Ir al contenido principal

Área de figuras combinadas / Ejercicios

De

Analiza el siguiente ejercicio.

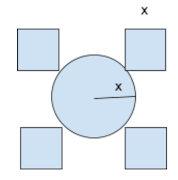
Humberto es un organizador de eventos, necesita realizar una alfombra de flores con forma de cuatro cuadrados y un círculo como se ve a continuación. 


Para la primera capa necesita aserrín, así que desea saber cuánto le costará rellenar la superficie. El metro cuadrado de aserrín cuesta $28 pesos.




¿Cuál es el modelo matemático que representa lo que gastará Humberto para cubrir la superficie?


Decir modelo matemático es buscar las fórmulas que nos ayudan a resolver el problema sin ejecutarlo.


La figura está conformada por 4 cuadrados y un círculo, por lo que se necesitan esas dos fórmulas.


Área del círculo = Π·R2


Área del cuadrado = L·L


Para obtener el área de uno de los cuadrados se sustituyen los valores.


Área del cuadrado= 2.5 x 2.5. 

Esto se multiplica por 4 ya que son 4 cuadrados.


4(2.5 x 2.5)

Otra forma de verle en forma reducida es


4(2.52)


Se sustituyen los valores en la fórmula para obtener el área del círculo

Área del círculo = Π·R2


Π·2.52


Ya tenemos nuestras dos áreas las unimos


Superficie total = 4(2.52) + (Π·2.52)


De estas dos fórmulas se obtiene el total de metros cuadrados de la superficie, el último paso es multiplicar por el costo del metro cuadrado de aserrín. 


28[ 4(2.52) + (Π·2.52)]  --- Este es el modelo matemático para resolver el problema.



para-recordar.png

En el CENEVAL es normal trabajar con problemas donde se cambie el valor por alguna incógnita.


Pero reconociendo las fórmulas de perímetro, área y volumen,  se puede identificar la aplicación correcta del modelo. Se sustituye “x” en lugar de 2.5.  


28[ 4(x2) + (Π·x2)] 


Ver este ejercicio en video.









Etiquetas:

Comentarios

Publicar un comentario

Entradas populares de este blog

Resolver problemas a través de un sistema de ecuaciones

De
Cada vez que un  jugador  gana una partida de dominó recibe 7 dólares y cada vez que pierde paga 3 dólares. Armamos nuestro sistema de ecuaciones: 7x - 3y = 55 Ahora resolvemos nuestro sistema despejamos c en la primera ecuación: Entonces se ganaron  10 partidas. 7(15 - y) - 3y = 55 105 -7y - 3y = 55 -10y = 55 - 105 y = -50/-10 y = 5 x = 10 ◦    Un número cualquiera --> x  (en realidad puede ser cualquier letra, el chiste está en que representa que desconocemos cuánto vale ese número) ◦    Otro número cualquiera --> y  (el problema habla de dos números que no se conocen, pero diferentes entre ellos, por eso a uno lo nombre "x" y al otro "y") ◦    Un número excede en  12   unidades  a otro  -->  x = y+ 12 , con esto estoy diciendo que si le sumo  12  a "y" será igual a "x" porque el problema dice que uno excede al otro en  12 unidades ◦...
Publicar un comentario
Leer más

Problemas del máximo común divisor

De
El máximo común divisor consiste en encontrar el divisor más grande de varios números. Por ejemplo para repartir cajas de naranjas, sin que sobren. Problema 1: Un comerciante desea poner en cajas 12,028 manzanas y 12,772  naranjas , de modo que cada caja contenga el mismo número de manzanas o  naranjas  y, además, el mayor número posible de ambas.  Hallar el número de  naranjas  de cada caja y el número de cajas necesarias para empaquetar toda la fruta. Problema 2: Un carpintero quiere cortar una plancha de madera de 256 cm de largo y 96 cm de ancho, en  cuadrados  lo más grandes posible. ¿Cuál debe ser la longitud del lado de cada cuadrado? y ¿cuántos  cuadrados  se obtienen de la plancha de madera? 
Publicar un comentario
Leer más

Resolución de problemas a través de un sistema de ecuaciones

De
Un número excede en 12 unidades a otro, si restáramos 4 unidades a cada uno de ellos entonces el primero seria igual al doble del segundo. ◦    Un número cualquiera --> x  (en realidad puede ser cualquier letra, el chiste está en que representa que desconocemos cuánto vale ese número) ◦    Otro número cualquiera --> y  (el problema habla de dos números que no se conocen, pero diferentes entre ellos, por eso a uno lo nombre "x" y al otro "y") ◦    Un número excede en 12 unidades a otro  -->  x = y+12 , con esto estoy diciendo que si le sumo 12 a "y" será igual a "x" porque el problema dice que uno excede al otro en 12 unidades ◦    Si restáramos 4 unidades a cada uno de ellos, entonces el primero sería igual al doble del segundo  -->  x - 4 = 2 (y - 4) Arriba tenemos ya nuestras dos ecuaciones y podemos resolver: ◦   x = y + 12 ◦   x - 4 = 2 (y - 4) Sustituyo el valor...
Publicar un comentario
Leer más